【SEOテキスト】宇田雄一「古典物理学」2-3-3逐次静止系,まず、以下の二つの定理①②が成り立つ。①∀t∈R({4});∀n∈N;∀k∈{1,・・・,n};∀m∈R(2×{1,・・・,n});∀f∈F2,n;【1】⇒【2】【1】∂4f(t,□,k)=0【2】∀r∈N;∀Z∈F4,r;∀i∈3;e5(t,i,k;f,Z(N3),m)=e1(t,i;f(N1,k),Z,0,m(□,k))②∀t∈R({4});∀n∈N;∀k∈{1,・・・,n};∀f∈F2,n;【1】⇒【2】【1】|∂4f(t,□,k)|<1【2】∃Λ∈L↑+;∃ξ∈N01;∃t'∈R({4});【2a】and【2b】and【2c】【2a】t(4)=ξ(4)and
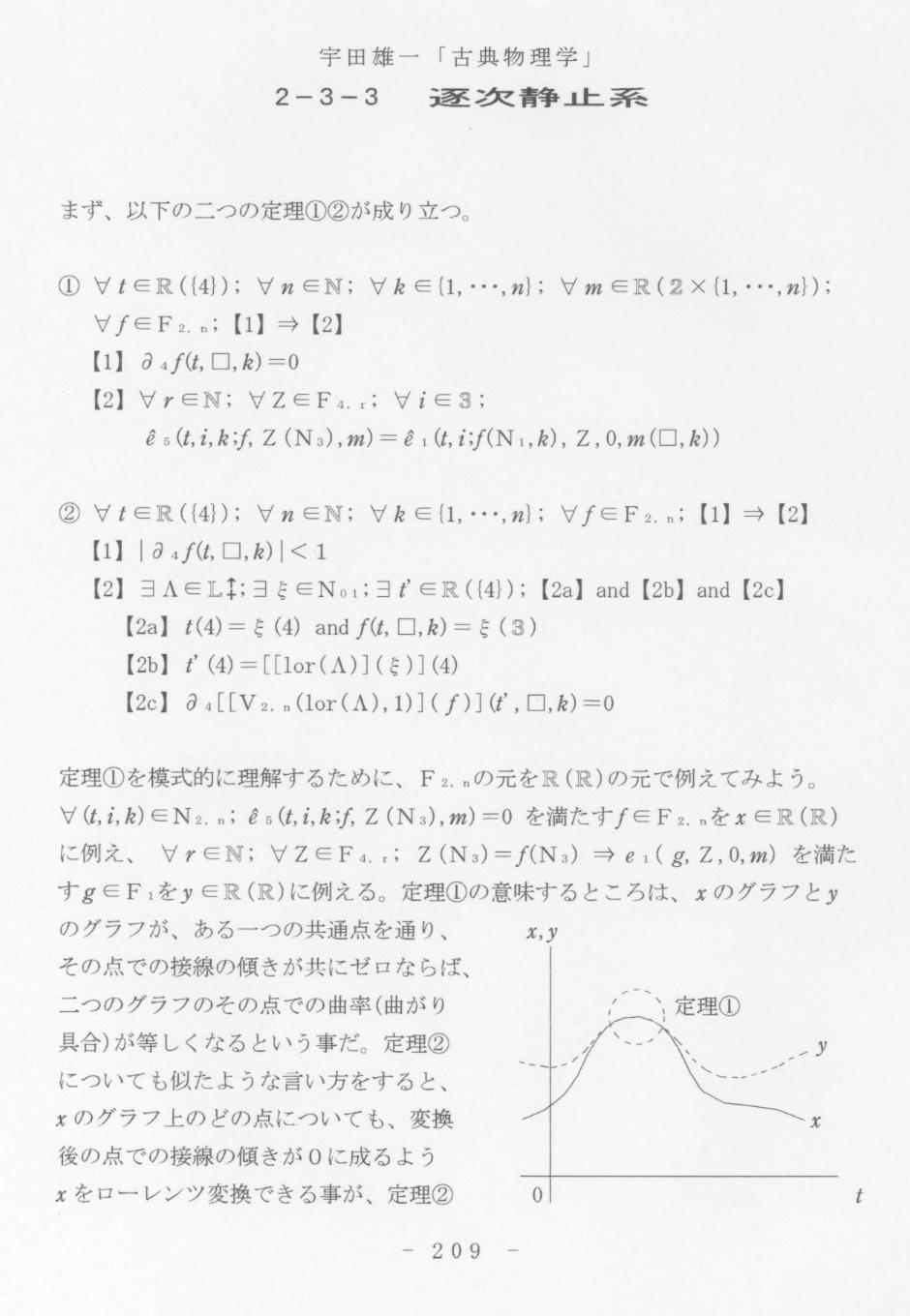
f(t,□,k)=ξ(3)【2b】t'(4)=[[lor(Λ)](ξ)](4)【2c】∂4[[V2,n(lor(Λ),1)](f)](t',□,k)=0定理①を模式的に理解するために、F2,nの元をR(R)の元で例えてみよう。∀(t,i,k)∈N2,n;e5(t,i,k;f,Z(N3),m)=0を満たすf∈F2,nをx∈R(R)に例え、∀r∈N;∀Z∈F4,r;Z(N3)=f(N3)⇒e1(g,Z,0,m)を満たすg∈F1をy∈R(R)に例える。定理①の意味するところは、xのグラフとyのグラフが、ある一つの共通点を通り、その点での接線の傾きが共にゼロならば、二つのグラフのその点での曲率(曲がり具合)が等しくなるという事だ。定理②についても似たような言い方をすると、xのグラフ上のどの点についても、変換後の点での接線の傾きが0に成るようxをローレンツ変換できる事が、定理②,x,y,定理①,y,x,0,t
|