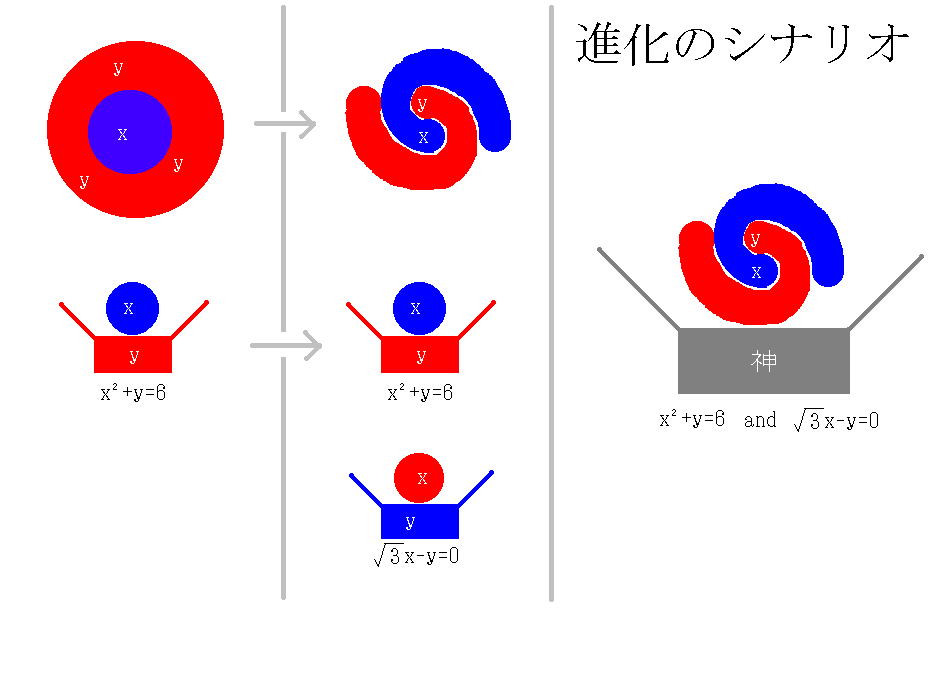
【SEOテキスト】宇田雄一「古典物理学」以前の方程式x2+y=6をそのまま持って来て、これを(x,y)に対する方程式と捉え直し、これを第3段階以後での法則だとすることが考えられる。しかしここでは、x2+y=6にもう一つの方程式を付け加えて、(x,y)=(√3,3)を解に持つ連立方程式を作り、これを第3段階以後での法則だとすることを考えてみる。例えば、(x2+y=6
and √3x-y=0)を法則とすることが考えられる。第2段階以後第3段階以前の、人間臭い言い方を用いれば、第3段階で付け加えられた方程式√3x-y=0は、環境条件xの下でのyに対する法則だと言うことが出来る。この見方をとれば、(x,y)に対する法則は、環境条件yの下でのxに対する法則と、環境条件xの下でのyに対する法則の二つから成り立ち、xとyが互いにいかなる影響を及ぼし合うかを記述するものと言える。第1段階以後第2段階以前ではx=-√3も解だったが、第3段階以後では(x,y)=(-√3,3)は解でない。これについても、もしy=3だったならx=-√3も可能だがxを√3から(-√3)へ変更するとその影響でyが3からずれてしまうので(x,y)=(-√3,3)は不可能だ。と解釈することが出来る。第3段階が一応は進化の最終段階だが、もし、(x,y)によって表されるのが自然全体の歴史ではなく自然の部分の歴史だと考えるならば、もう一度第2段階と第3段階の手続きを繰り返して、さらなる進化を期待できる。もっと進化した理論を作りたければ、この手続きをもっと繰り返せばよい。最初から自然全体の歴史が(x,y)によって表されることを知っているのに、わざとxを可変的,yを固定的と見てxに対する法則を探したり、yを可変的,xを固定的と見てyに対する法則を探したりして、それらを組み合わせて(x,y)に対する法則を作り上げるという方法がある。この方法は「分析と総合」と呼ばれる。また、xを可変的と見る理論が進化して(x,y)を可変的と見る理論が生まれる行き方の他に、yを可変的と見る理論が進化して(x,y)を可変的と見る理論が生まれる行き方もある。この二つの成り行きの違いは、xを幹と見てyを枝と見るのか、yを幹と見てxを枝と見るのかの違いに例えられるだろう。
|